一、探知究竟
例题:某公司筹办的年度晚会节目包括4个小品,3个演唱和3个舞蹈,为便于对节目进行评选,要求同类型的节目必须连续出现,那么共有多少种出场顺序?
A.5184
B.2160
C.3768
D.4372
【解析】A。要求“同类型的节目连续出现”。那如何能保证相同类型的节目一定会连续出现呢?那就是用前文提到的“捆绑法”。既然要求相同类型的连续,那我们不妨将每一个类型看成一个整体。针对本题就是三类节目分别看成3个整体。那接下来这三个整体各自内部需不需要考虑顺序呢?
即使是同类型的节目看成一个整体,但每个具体节目是不还都不一样了,所以内部需要考虑顺序,因此三类节目捆绑后依次的情况数为: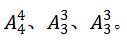 现在三类节目分别看成一个整体了,但是每个整体谁前谁后是不同样也需要考虑顺序,故三个整体考虑顺序的情况数:
现在三类节目分别看成一个整体了,但是每个整体谁前谁后是不同样也需要考虑顺序,故三个整体考虑顺序的情况数: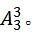 最后不管是前面捆绑的过程还是捆绑完成后排序的过程都为完成整件事中的某一步,所以分步用乘,最终结果为:
最后不管是前面捆绑的过程还是捆绑完成后排序的过程都为完成整件事中的某一步,所以分步用乘,最终结果为: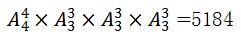 (结合选项可知结果数比较大,尾数各不相同,可快速算尾数确定答案)。故本题选A。
(结合选项可知结果数比较大,尾数各不相同,可快速算尾数确定答案)。故本题选A。
二、总结方法
1、先确定题目是否适用捆绑法。如有“某部分元素必须相邻”的要求时,即可考虑使用捆绑法。
2、使用捆绑法时,先将有“相邻”要求的元素捆绑成一个整体,再考虑捆绑后的整体内部需不需要考虑次序-----结合题目具体分析。
3、捆绑后的整体和其他元素再进行排列-----同样结合题目具体分析需不需要考虑次序。
结合例题来看,此类排列组合题目难度适当,具有明显的特征。确定好题型后按照方法步骤,一步一步解题即可。希望大家多刷题,做到心中有数,下笔有神。


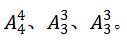 现在三类节目分别看成一个整体了,但是每个整体谁前谁后是不同样也需要考虑顺序,故三个整体考虑顺序的情况数:
现在三类节目分别看成一个整体了,但是每个整体谁前谁后是不同样也需要考虑顺序,故三个整体考虑顺序的情况数: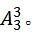 最后不管是前面捆绑的过程还是捆绑完成后排序的过程都为完成整件事中的某一步,所以分步用乘,最终结果为:
最后不管是前面捆绑的过程还是捆绑完成后排序的过程都为完成整件事中的某一步,所以分步用乘,最终结果为: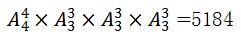 (结合选项可知结果数比较大,尾数各不相同,可快速算尾数确定答案)。故本题选A。
(结合选项可知结果数比较大,尾数各不相同,可快速算尾数确定答案)。故本题选A。